Maximal Update Parametrization (μP) - coordinate checking
The purpose of this notebook is to illustrate the correctness of the MuLinear and Cerebras compatible μP implementations. This is done by calculating the average size of coordinates for a few training steps across the varying model widths for (a) pre-activation layers, (b) model weights, and (c) changes in model weights.
[1]:
import logging
import math
import warnings
from collections.abc import Callable
from typing import Any, Literal
import lightning.pytorch as pl
import matplotlib.pyplot as plt
import seaborn as sns
import torch
import torch.nn.functional as F
from torch import nn
from torchvision import datasets, transforms
from cellarium.ml.layers import MuLinear
from cellarium.ml.utilities.layers import create_initializer, scale_initializers_by_dimension
from cellarium.ml.utilities.mup import LRAdjustmentGroup
from cellarium.ml.utilities.testing import get_coord_data
logging.getLogger("lightning.pytorch").setLevel(logging.ERROR)
Data processing
The models are trained on CIFAR-10 dataset.
[2]:
data_dir = "/tmp"
batch_size = 64
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
trainset = datasets.CIFAR10(root=data_dir, train=True, download=True, transform=transform)
train_loader = torch.utils.data.DataLoader(trainset, batch_size=batch_size, shuffle=True)
Files already downloaded and verified
Model definitions
A simple 2-hidden-layer MLP with SP and muP. Notice that at base width Standard and μ Parametrizatons are identical. MLP with SP is given in [1].
[ ]:
# SP MLP
class MLP(pl.LightningModule):
def __init__(
self,
width: int = 128,
num_classes: int = 10,
bias: bool = False,
nonlin: Callable[[torch.Tensor], torch.Tensor] = F.relu,
input_mult: float = 1.0,
output_mult: float = 1.0,
loss_fn: Callable[[torch.Tensor, torch.Tensor], torch.Tensor] = F.cross_entropy,
optim_fn: type[torch.optim.Optimizer] = torch.optim.Adam,
lr: float = 0.01,
eps: float = 1e-8,
weight_decay: float = 0.01,
) -> None:
super().__init__()
self.width = width
self.bias = bias
self.nonlin = nonlin
self.input_mult = input_mult
self.output_mult = output_mult
self.loss_fn = loss_fn
self.optim_fn = optim_fn
self.lr = lr
self.eps = eps
self.weight_decay = weight_decay
self.fc_1 = nn.Linear(3072, width, bias=bias)
self.fc_2 = nn.Linear(width, width, bias=bias)
self.fc_3 = nn.Linear(width, num_classes, bias=bias)
self.reset_parameters()
def reset_parameters(self) -> None:
fan_in_1 = self.fc_1.weight.shape[1]
nn.init.normal_(self.fc_1.weight, std=1 / math.sqrt(fan_in_1)) # 1 / sqrt(d)
self.fc_1.weight.data /= self.input_mult
fan_in_2 = self.fc_2.weight.shape[1]
nn.init.normal_(self.fc_2.weight, std=1 / math.sqrt(fan_in_2)) # 1 / sqrt(n)
nn.init.zeros_(self.fc_3.weight) # zero readout
if self.bias:
# zero biases
nn.init.zeros_(self.fc_1.bias)
nn.init.zeros_(self.fc_2.bias)
nn.init.zeros_(self.fc_3.bias)
def forward(self, x: torch.Tensor) -> torch.Tensor:
x = self.nonlin(self.fc_1(x) * self.input_mult)
x = self.nonlin(self.fc_2(x))
return self.fc_3(x) * self.output_mult
def training_step(self, batch: tuple[torch.Tensor, torch.Tensor], batch_idx: int) -> torch.Tensor:
data, target = batch
output = self(data.view(data.size(0), -1))
loss = self.loss_fn(output, target)
return loss
def configure_optimizers(self) -> torch.optim.Optimizer:
optim_kwargs: dict[str, Any] = {"lr": self.lr}
if self.optim_fn in [torch.optim.Adam, torch.optim.AdamW]:
optim_kwargs["eps"] = self.eps
if self.optim_fn == torch.optim.AdamW:
optim_kwargs["weight_decay"] = self.weight_decay
return self.optim_fn(self.parameters(), **optim_kwargs)
# muP MLP (MuLinear backend)
# Note: MuLinear layer automatically handles the scaling of the weights and learning rates
# The learning rate for individual layers are adjusted via internal parameter multipliers
# Gradients for Adam and AdamW are scaled via the hook in the parameters
class MuLinearMLP(pl.LightningModule):
def __init__(
self,
width: int = 128,
num_classes: int = 10,
bias: bool = False,
nonlin: Callable[[torch.Tensor], torch.Tensor] = F.relu,
optimizer: Literal["sgd", "adam", "adamw"] = "sgd",
input_mult: float = 1.0,
output_mult: float = 1.0,
loss_fn: Callable[[torch.Tensor, torch.Tensor], torch.Tensor] = F.cross_entropy,
optim_fn: type[torch.optim.Optimizer] = torch.optim.Adam,
lr: float = 0.01,
eps: float = 1e-8,
weight_decay: float = 0.01,
) -> None:
super().__init__()
self.width = width
self.bias = bias
self.nonlin = nonlin
self.input_mult = input_mult
self.output_mult = output_mult
self.loss_fn = loss_fn
self.optim_fn = optim_fn
self.lr = lr
self.eps = eps
self.weight_decay = weight_decay
self.fc_1 = MuLinear(
in_features=3072,
out_features=width,
bias=bias,
layer="input",
optimizer=optimizer,
weight_init_std=(1 / (math.sqrt(3072) * self.input_mult)),
base_width=128,
)
self.fc_2 = MuLinear(
in_features=width,
out_features=width,
bias=bias,
layer="hidden",
optimizer=optimizer,
weight_init_std=(1 / math.sqrt(128)),
base_width=128,
)
self.fc_3 = MuLinear(
in_features=width,
out_features=num_classes,
bias=bias,
layer="output",
optimizer=optimizer,
weight_init_std=0.0,
base_width=128,
)
def forward(self, x: torch.Tensor) -> torch.Tensor:
x = self.nonlin(self.fc_1(x) * self.input_mult)
x = self.nonlin(self.fc_2(x))
return self.fc_3(x) * self.output_mult
def training_step(self, batch: tuple[torch.Tensor, torch.Tensor], batch_idx: int) -> torch.Tensor:
data, target = batch
output = self(data.view(data.size(0), -1))
loss = self.loss_fn(output, target)
return loss
def configure_optimizers(self) -> torch.optim.Optimizer:
optim_kwargs: dict[str, Any] = {"lr": self.lr}
if self.optim_fn in [torch.optim.Adam, torch.optim.AdamW]:
optim_kwargs["eps"] = self.eps
if self.optim_fn == torch.optim.AdamW:
optim_kwargs["weight_decay"] = self.weight_decay
return self.optim_fn(self.parameters(), **optim_kwargs)
# muP MLP (Cerebras compatible)
# Note: This implementation explicitly handles the scaling of the weights and learning rates
# The learning rate for individual layers are adjusted via LRAdjustmentGroup
# Since the weight decay is coupled with the learning rate in AdamW, we need to decouple it
# by scaling it inversely with the learning rate.
# Also instead of scaling the gradients, here we scale down the eps for Adam and AdamW
class CerebrasMLP(pl.LightningModule):
def __init__(
self,
width: int = 128,
num_classes: int = 10,
bias: bool = False,
nonlin: Callable[[torch.Tensor], torch.Tensor] = F.relu,
input_mult: float = 1.0,
output_mult: float = 1.0,
loss_fn: Callable[[torch.Tensor, torch.Tensor], torch.Tensor] = F.cross_entropy,
optim_fn: type[torch.optim.Optimizer] = torch.optim.Adam,
lr: float = 0.01,
eps: float = 1e-8,
weight_decay: float = 0.01,
) -> None:
super().__init__()
self.width = width
self.bias = bias
self.nonlin = nonlin
self.input_mult = input_mult
self.output_mult = output_mult
self.loss_fn = loss_fn
self.optim_fn = optim_fn
self.lr = lr
self.eps = eps
self.weight_decay = weight_decay
self.fc_1 = nn.Linear(3072, width, bias=bias)
self.fc_2 = nn.Linear(width, width, bias=bias)
self.fc_3 = nn.Linear(width, num_classes, bias=bias)
self.fc_1_initializer = {"name": "normal_", "mean": 0.0, "std": 1 / (math.sqrt(3072) * self.input_mult)}
self.fc_2_initializer = {"name": "normal_", "mean": 0.0, "std": 1 / math.sqrt(128)}
self.fc_3_initializer = {"name": "zeros_"}
width_mult = width / 128
scale_initializers_by_dimension(
self.fc_2_initializer,
width_scale=width_mult**-0.5,
)
self.output_mult /= width_mult
self.width_mult = width_mult
self.lr_adjustment_groups = {"fc_2": LRAdjustmentGroup("*fc_2*weight")}
self.lr_adjustment_groups["fc_2"].set_scale(1 / width_mult)
self.reset_parameters()
def reset_parameters(self) -> None:
create_initializer(self.fc_1_initializer)(self.fc_1.weight)
create_initializer(self.fc_2_initializer)(self.fc_2.weight)
create_initializer(self.fc_3_initializer)(self.fc_3.weight)
if self.bias:
# zero biases
nn.init.zeros_(self.fc_1.bias)
nn.init.zeros_(self.fc_2.bias)
nn.init.zeros_(self.fc_3.bias)
def forward(self, x: torch.Tensor) -> torch.Tensor:
x = self.nonlin(self.fc_1(x) * self.input_mult)
x = self.nonlin(self.fc_2(x))
return self.fc_3(x) * self.output_mult
def training_step(self, batch: tuple[torch.Tensor, torch.Tensor], batch_idx: int) -> torch.Tensor:
data, target = batch
output = self(data.view(data.size(0), -1))
loss = self.loss_fn(output, target)
return loss
def configure_optimizers(self) -> torch.optim.Optimizer:
# Group parameters by learning rate adjustment group
params_groups_dict: dict[str, list[torch.Tensor]] = {}
for name, param in self.named_parameters():
for lr_group_name, lr_group in self.lr_adjustment_groups.items():
if lr_group.param_filter(name):
params_groups_dict.setdefault(lr_group_name, []).append(param)
break
else:
params_groups_dict.setdefault("default", []).append(param)
# Create parameter groups for the optimizer
param_groups = []
for lr_group_name, params in params_groups_dict.items():
group_optim_kwargs = {"lr": self.lr, "eps": self.eps / self.width_mult}
if self.optim_fn == torch.optim.AdamW:
group_optim_kwargs["weight_decay"] = self.weight_decay
if lr_group_name != "default":
group_optim_kwargs["lr"] *= self.lr_adjustment_groups[lr_group_name].scale
if self.optim_fn == torch.optim.AdamW:
# weight_decay is coupled with the learning rate in AdamW
# so we need to decouple it by scaling it inversely with the learning rate
# see https://github.com/microsoft/mup/issues/1
group_optim_kwargs["weight_decay"] /= self.lr_adjustment_groups[lr_group_name].scale
param_groups.append({"params": params, **group_optim_kwargs})
return self.optim_fn(param_groups, **{})
Checking coordinate statistics
Following are the scaling rules for μP (Appendix J.2 of [1]):
Pre-activation layers (outputs): \(\Theta(1)\)
Input weights: \(W = \Theta(1)\) and \(\Delta W = \Theta(1)\)
Hidden weights: \(W = \Theta(1 / \sqrt{n})\) and \(\Delta W = \Theta(1 / n)\)
Output weights: \(W = \Theta(1 / n)\) and \(\Delta W = \Theta(1 / n)\)
All biases: \(b = \Theta(1)\) and \(\Delta b = \Theta(1)\)
[4]:
optim_dict = {"sgd": torch.optim.SGD, "adam": torch.optim.Adam, "adamw": torch.optim.AdamW}
# adapted from https://github.com/microsoft/mup/blob/main/examples/MLP/main.py
def coord_check_MLP(
implementation: Literal["sp", "mup_mu_linear", "mup_cerebras"],
bias: bool,
nonlin: Callable[[torch.Tensor], torch.Tensor],
lr: float,
input_mult: float,
output_mult: float,
optim_name: Literal["adam", "adamw"],
train_loader: torch.utils.data.DataLoader,
nsteps: int,
nseeds: int,
widths: list[int],
) -> None:
optim_fn = optim_dict[optim_name]
def gen(w: int) -> Callable[[], pl.LightningModule]:
def f() -> pl.LightningModule:
model: pl.LightningModule
if implementation == "sp":
model = MLP(
width=w,
bias=bias,
nonlin=nonlin,
input_mult=input_mult,
output_mult=output_mult,
loss_fn=F.cross_entropy,
optim_fn=optim_fn,
lr=lr,
)
elif implementation == "mup_mu_linear":
model = MuLinearMLP(
width=w,
bias=bias,
nonlin=nonlin,
optimizer=optim_name,
input_mult=input_mult,
output_mult=output_mult,
loss_fn=F.cross_entropy,
optim_fn=optim_fn,
lr=lr,
)
elif implementation == "mup_cerebras":
model = CerebrasMLP(
width=w,
bias=bias,
nonlin=nonlin,
input_mult=input_mult,
output_mult=output_mult,
loss_fn=F.cross_entropy,
optim_fn=optim_fn,
lr=lr,
)
return model
return f
models = {w: gen(w) for w in widths}
layer_name_to_multiplier_name = {"fc_1": "input_mult", "fc_3": "output_mult"}
with warnings.catch_warnings():
warnings.filterwarnings("ignore", message="The 'train_dataloader' does not have many workers")
df = get_coord_data(
models,
layer_name_to_multiplier_name,
train_loader,
nseeds=nseeds,
nsteps=nsteps,
)
# plot coordinates
fig = plt.figure(figsize=(5 * nsteps, 10 + bias * 6))
face_color = "xkcd:light grey" if implementation == "sp" else None
if face_color is not None:
fig.patch.set_facecolor(face_color)
n_rows = 3 + bias * 2
for t in range(nsteps):
df_t = df[df.t == t]
# outputs
plt.subplot(n_rows, nsteps, t + 1)
sns.lineplot(x="width", y="l1", data=df_t[(df_t.type == "out")], hue="module", legend=True if t == 0 else None)
plt.title(f"t={t}")
if t != 0:
plt.ylabel("")
plt.loglog(base=2, nonpositive="mask")
# parameter values
plt.subplot(n_rows, nsteps, t + 1 + nsteps)
sns.lineplot(
x="width",
y="l1",
data=df_t[(df_t.type == "param") & (df_t.module.str.contains("weight"))],
hue="module",
legend=True if t == 0 else None,
)
if t != 0:
plt.ylabel("")
plt.loglog(base=2, nonpositive="mask")
# parameter deltas
plt.subplot(n_rows, nsteps, t + 1 + nsteps * 2)
sns.lineplot(
x="width",
y="l1",
data=df_t[(df_t.type == "delta") & (df_t.module.str.contains("weight"))],
hue="module",
legend=True if t == 0 else None,
)
if t != 0:
plt.ylabel("")
plt.loglog(base=2, nonpositive="mask")
if bias:
# bias values
plt.subplot(n_rows, nsteps, t + 1 + nsteps * 3)
sns.lineplot(
x="width",
y="l1",
data=df_t[(df_t.type == "param") & (df_t.module.str.contains("bias"))],
hue="module",
legend=True if t == 0 else None,
)
if t != 0:
plt.ylabel("")
plt.loglog(base=2, nonpositive="mask")
# bias deltas
plt.subplot(n_rows, nsteps, t + 1 + nsteps * 4)
sns.lineplot(
x="width",
y="l1",
data=df_t[(df_t.type == "delta") & (df_t.module.str.contains("bias"))],
hue="module",
legend=True if t == 0 else None,
)
if t != 0:
plt.ylabel("")
plt.loglog(base=2, nonpositive="mask")
prm = "SP" if implementation == "sp" else "μP"
suptitle = f"{prm} MLP {optim_name} lr={lr} nseeds={nseeds}"
plt.suptitle(suptitle)
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
μP implementations differ for different optimizers, therefore, we have to check each optimizer separately.
Illustrating correctness of the μP implementation for the SGD optimizer
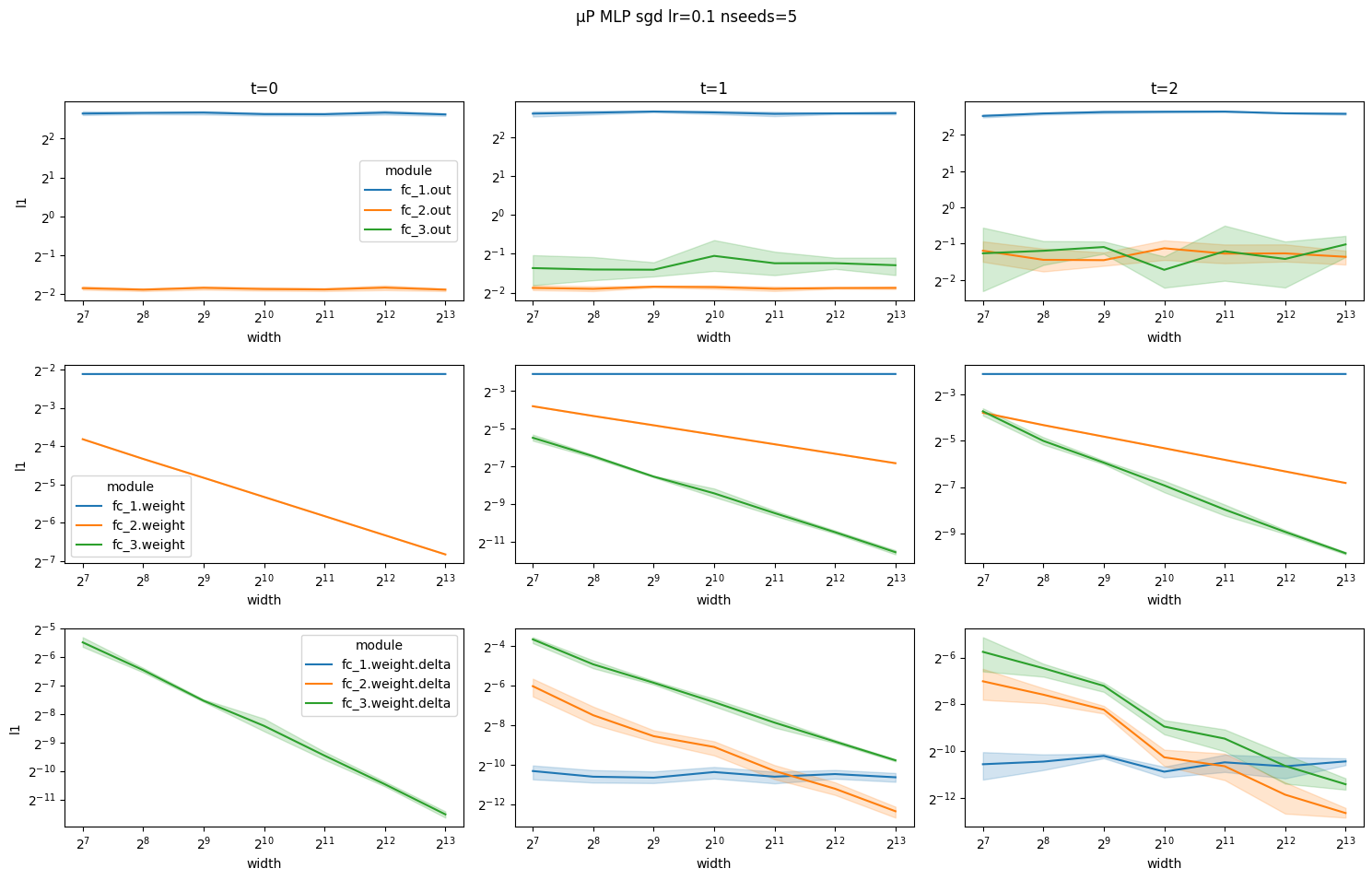
Notice how for the μP MLP coordinates scale with width according to the rules above at each time step. In particular, layer outputs are constant and do not explode with width.
[5]:
# optimal values for HPs at base width for SGD optimizer
# input_mult = 2**-4
# output_mult = 2**5
[6]:
# muP SGD (MuLinear)
coord_check_MLP(
implementation="mup_mu_linear",
bias=False,
nonlin=F.relu,
lr=0.1,
input_mult=2**-4,
output_mult=2**5,
optim_name="sgd",
train_loader=train_loader,
nsteps=3,
nseeds=5,
widths=[2**i for i in range(7, 14)],
)
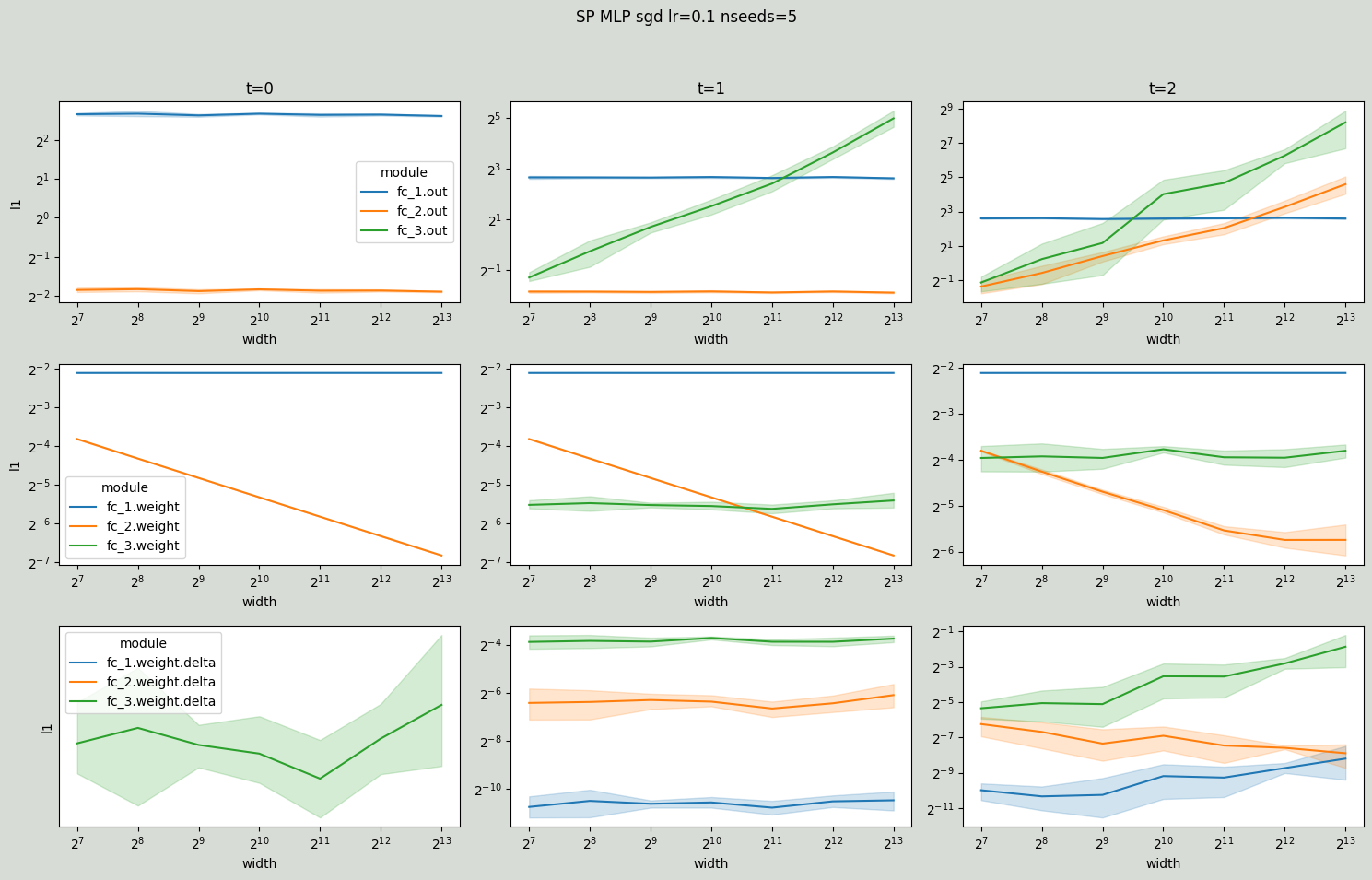
Now, notice how for SP MLP the layer outputs explode with width at time steps 1 and 2.
[7]:
# SP SGD
coord_check_MLP(
implementation="sp",
bias=False,
nonlin=F.relu,
lr=0.1,
input_mult=2**-4,
output_mult=2**5,
optim_name="sgd",
train_loader=train_loader,
nsteps=3,
nseeds=5,
widths=[2**i for i in range(7, 14)],
)
Illustrating correctness of the μP implementation for the Adam optimizer
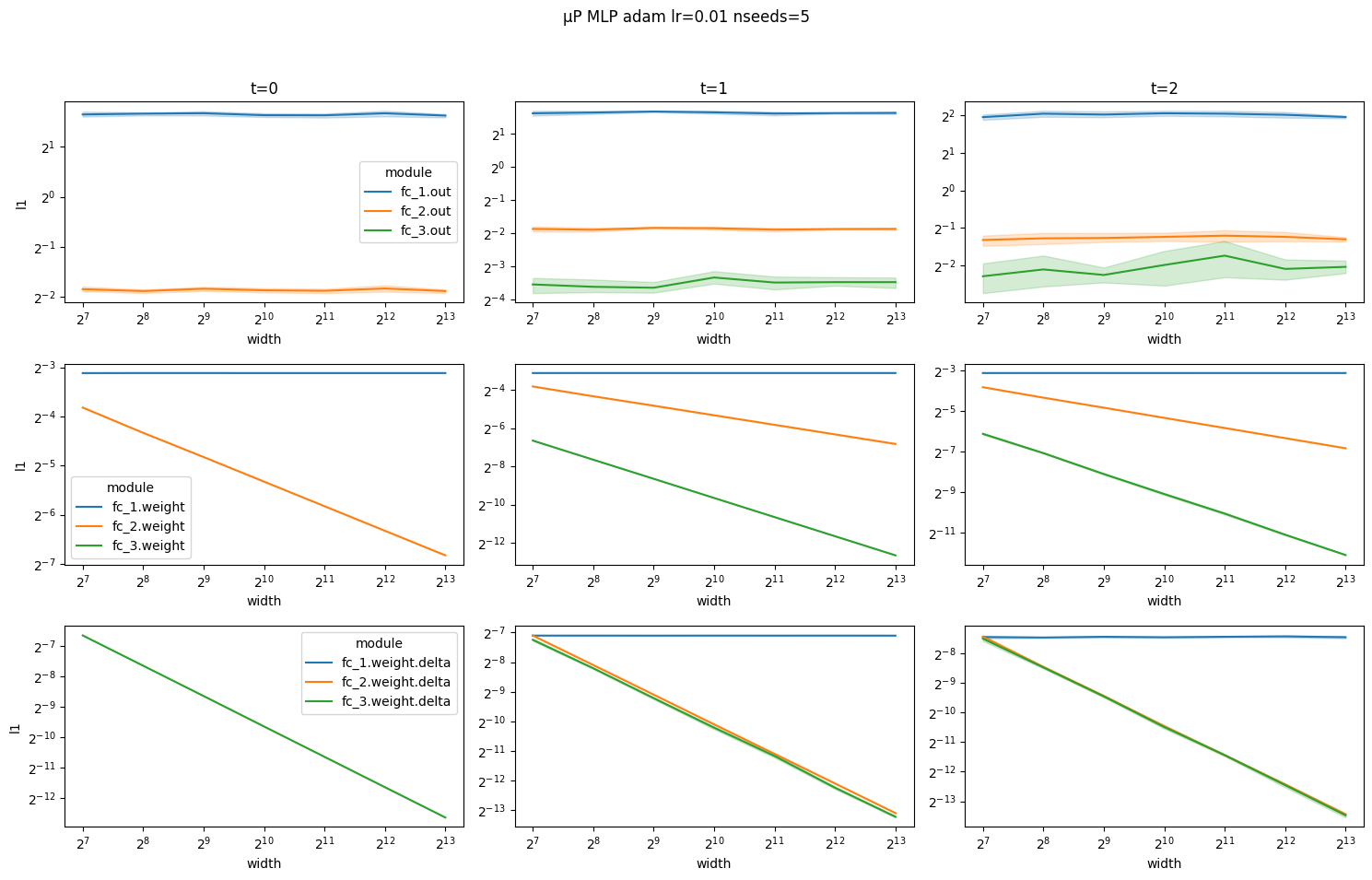
Again, notice how coordinates scale according to the μP scaling rules.
[8]:
# optimal values for HPs at base width for Adam optimizer
# input_mult = 2**-3
# output_mult = 2**-4
[9]:
# muP Adam (MuLinear)
coord_check_MLP(
implementation="mup_mu_linear",
bias=False,
nonlin=F.relu,
lr=0.01,
input_mult=2**-3,
output_mult=2**-4,
optim_name="adam",
train_loader=train_loader,
nsteps=3,
nseeds=5,
widths=[2**i for i in range(7, 14)],
)
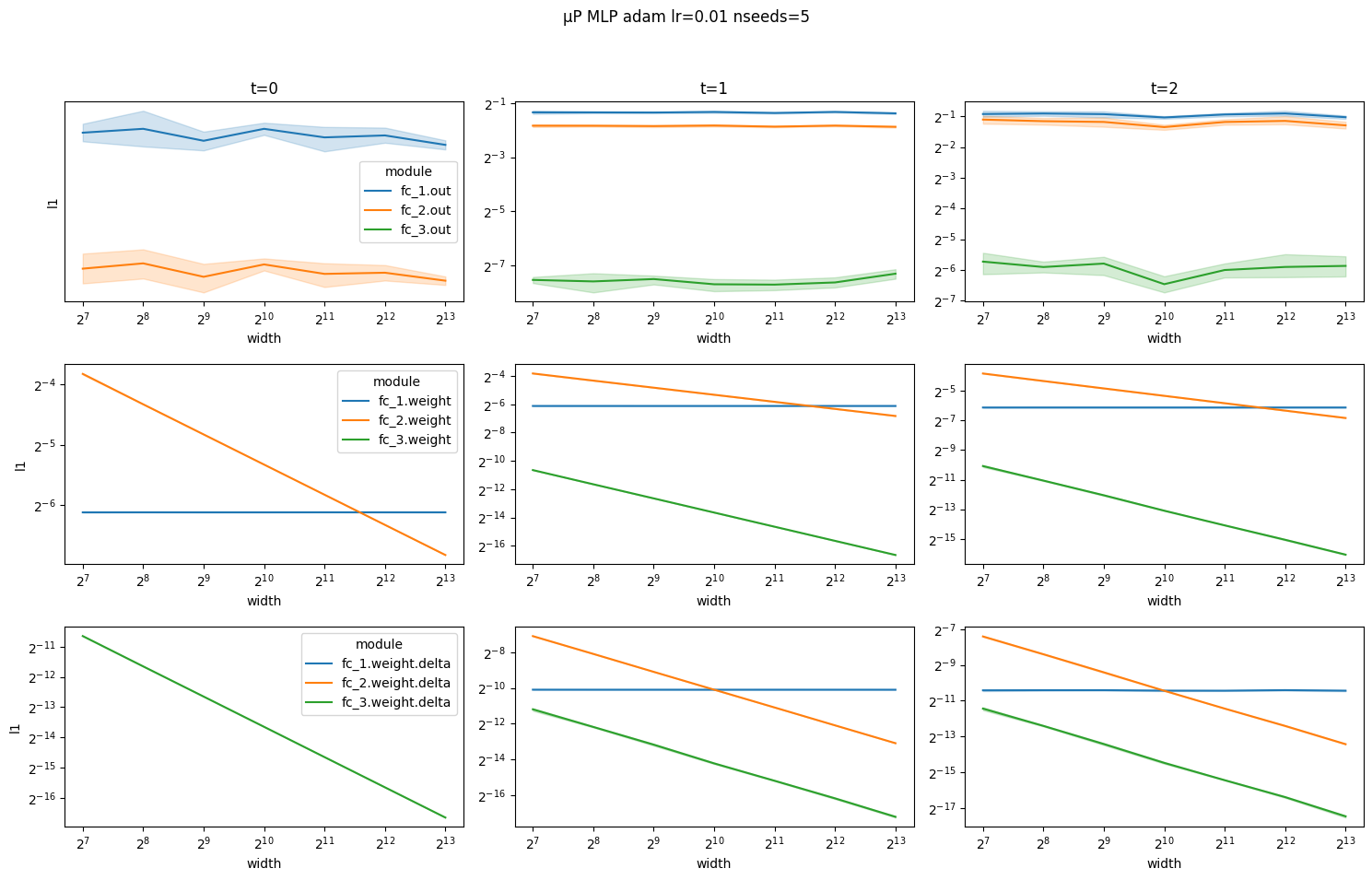
[10]:
# muP Adam (Cerebras compatible)
coord_check_MLP(
implementation="mup_cerebras",
bias=False,
nonlin=F.relu,
lr=0.01,
input_mult=2**-3,
output_mult=2**-4,
optim_name="adam",
train_loader=train_loader,
nsteps=3,
nseeds=5,
widths=[2**i for i in range(7, 14)],
)
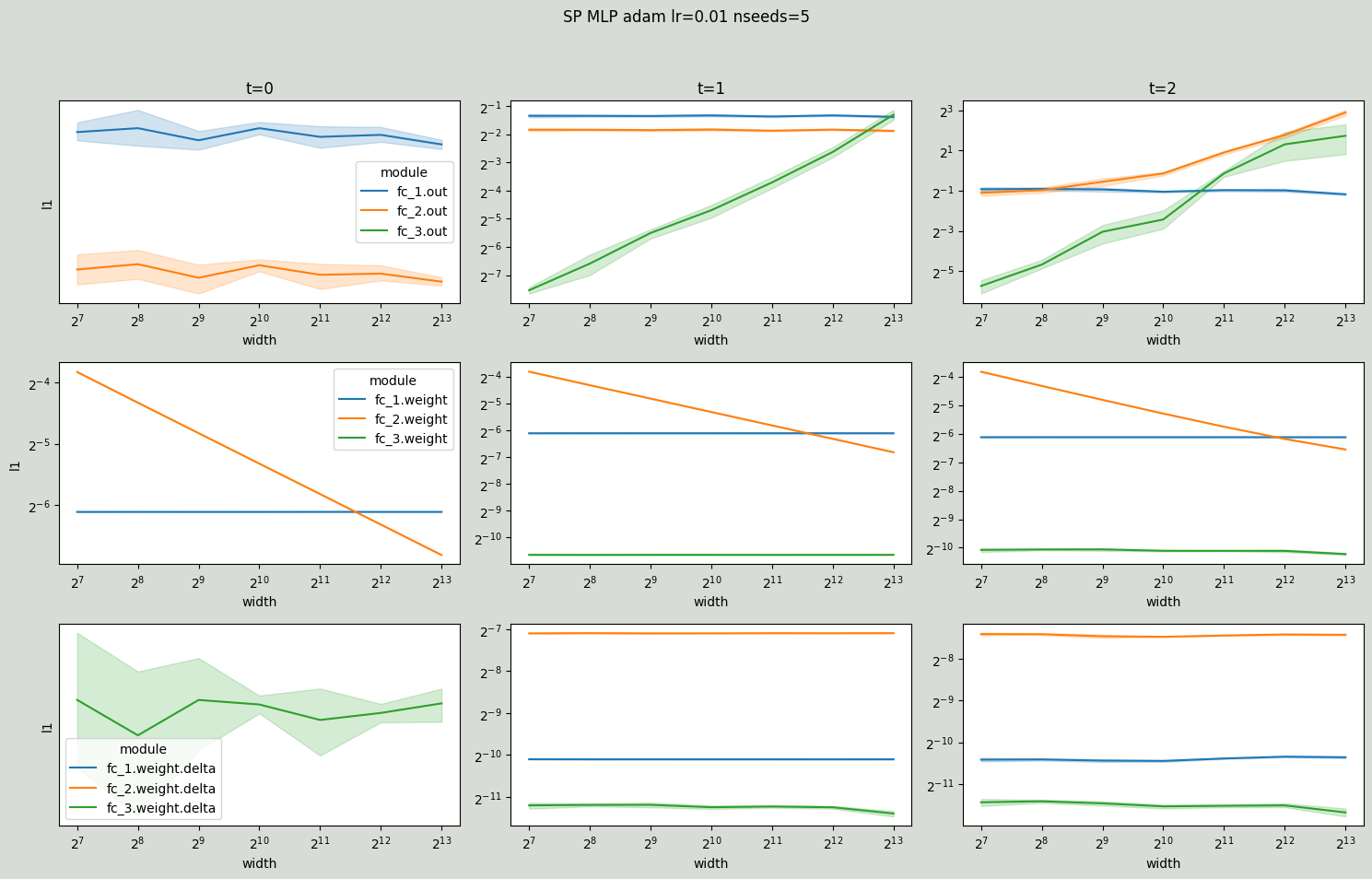
And layer outputs explode at time steps 1 and 2 for SP MLP.
[11]:
# SP Adam
coord_check_MLP(
implementation="sp",
bias=False,
nonlin=F.relu,
lr=0.01,
input_mult=2**-3,
output_mult=2**-4,
optim_name="adam",
train_loader=train_loader,
nsteps=3,
nseeds=5,
widths=[2**i for i in range(7, 14)],
)
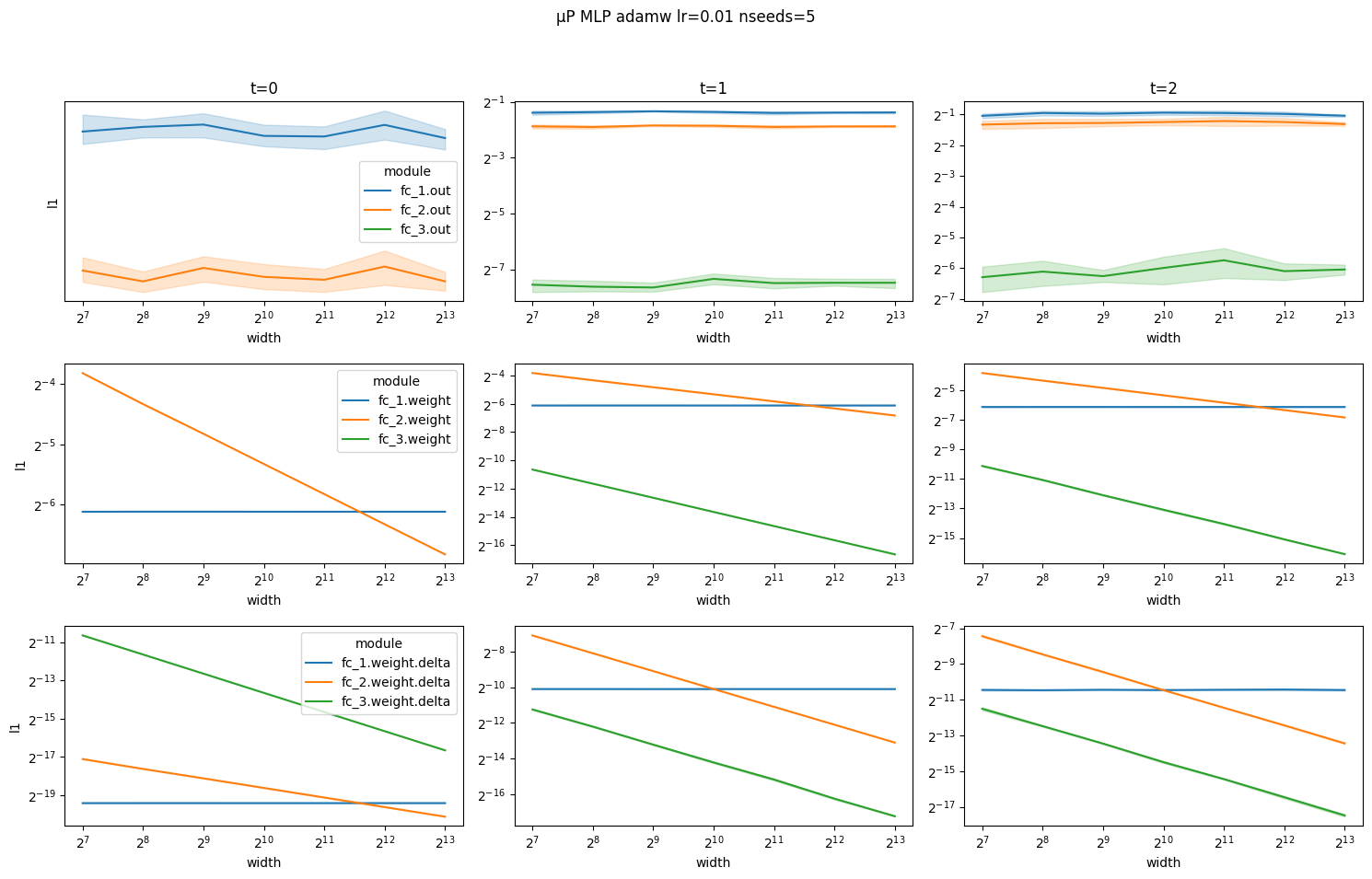
Illustrating correctness of the μP implementation for the AdamW optimizer
Same scaling rules apply for AdamW with one exception: for hidden layer weights ∆W is a combination of gradient updates Θ(1/n) and weight decay Θ(1/sqrt(n)) that scale differently. In particular, at time step 0 ∆W is only due to weight decay Θ(1/sqrt(n)) and at time steps 1 and 2 ∆W is dominated by the weight decay Θ(1/sqrt(n)).
[12]:
# muP AdamW (MuLinear)
coord_check_MLP(
implementation="mup_mu_linear",
bias=False,
nonlin=F.relu,
lr=0.01,
input_mult=2**-3,
output_mult=2**-4,
optim_name="adamw",
train_loader=train_loader,
nsteps=3,
nseeds=5,
widths=[2**i for i in range(7, 14)],
)
[13]:
# muP AdamW (Cerebras compatible)
coord_check_MLP(
implementation="mup_cerebras",
bias=False,
nonlin=F.relu,
lr=0.01,
input_mult=2**-3,
output_mult=2**-4,
optim_name="adamw",
train_loader=train_loader,
nsteps=3,
nseeds=5,
widths=[2**i for i in range(7, 14)],
)
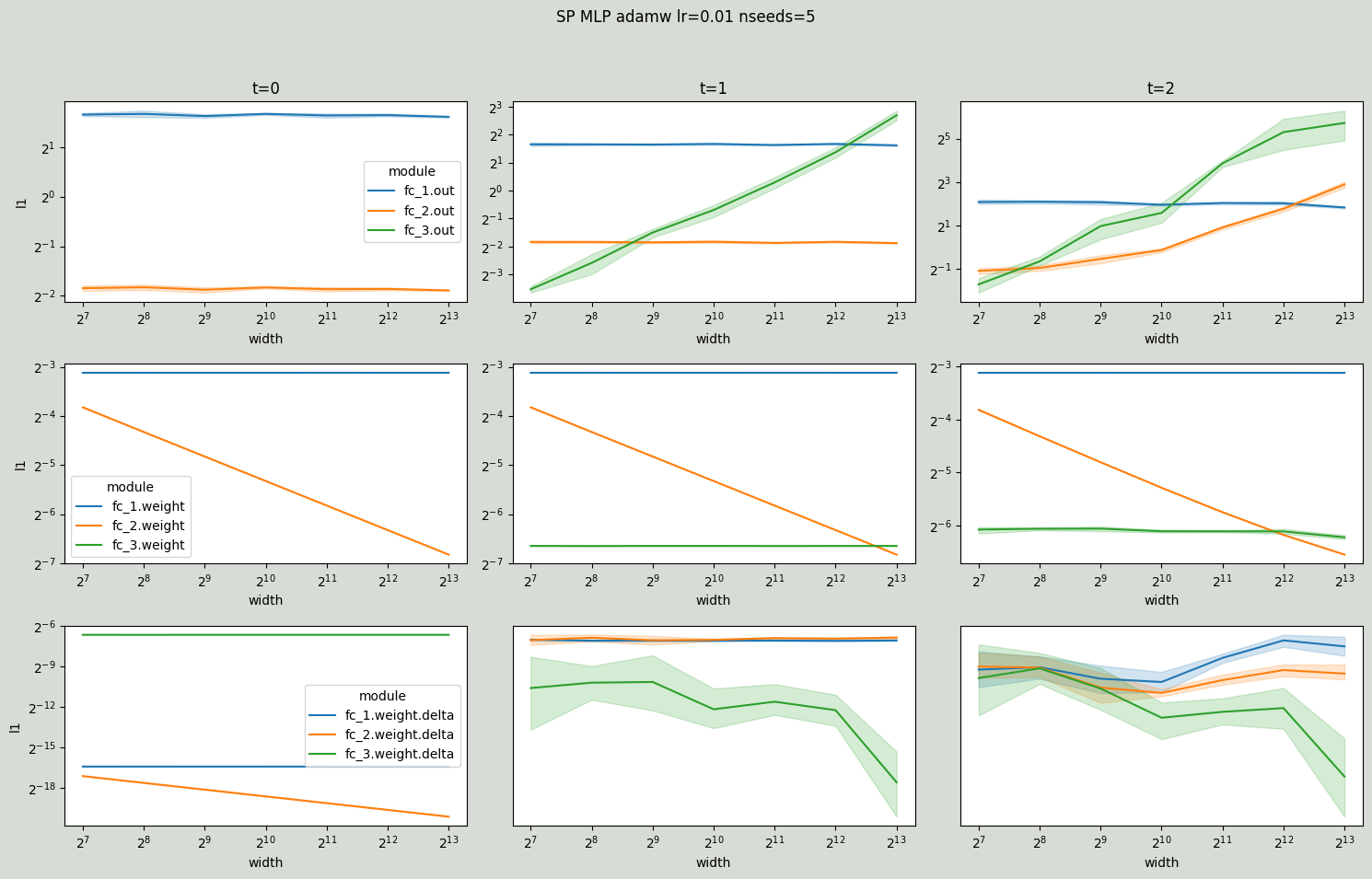
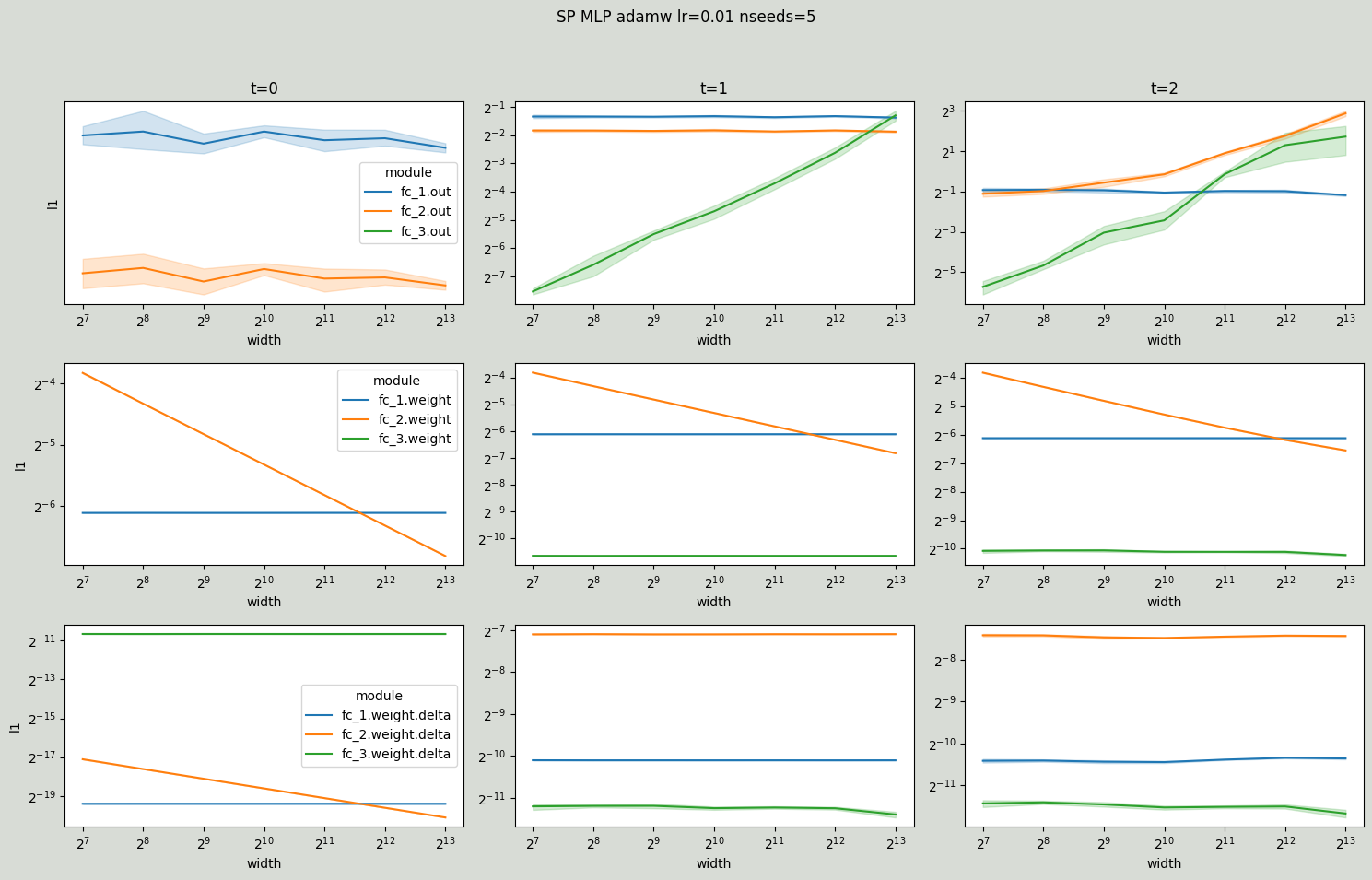
Again, for comparison SP MLP with exploding layer outputs.
[14]:
# SP AdamW
coord_check_MLP(
implementation="sp",
bias=False,
nonlin=F.relu,
lr=0.01,
input_mult=2**-3,
output_mult=2**-4,
optim_name="adamw",
train_loader=train_loader,
nsteps=3,
nseeds=5,
widths=[2**i for i in range(7, 14)],
)
References: